Product in categories
Given two objects $A$ and $B$ in a category, the product is another object $P$ together with two morphisms $\pi_1: P\mapsto A$ and $\pi_2: P\mapsto B$ that satisfy the following universal property: if $X$ is any other object in the category with morphisms $f_{1}: X \rightarrow A$ and $f_{2}: X \rightarrow B$ then there is an unique morphism $g: X \rightarrow P$ such that $f_1=\pi_1 \circ g$ and $f_2=\pi_2 \circ g$
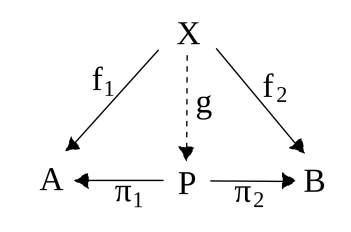
When the product exists is unique up to isomorphisms.
Examples
- Given the category of sets with morphisms the functions, the product of two sets $A$ and $B$ is the cartesian product $A\times B$ with the natural projection functions.
- For a set $S$ the powerset $\mathcal{P}(S)$ is a category whose morphisms are the inclusions. The product of two elements $A,B \in \mathcal{P}(S)$ is the intersection $A\cap B$
- Greatest common divisor and least common multiple are products in their respective categories of partial ordered sets.
- In the category of groups, the product is the direct product of groups (versus the semidirect product case)
___
More comments
The product is associative up to isomorphism, that is, given $A,B,C$ in the category we have
$$ (A \times B) \times C \cong A \times(B \times C) $$The product can be defined for $n$ objects in the category, including $n=1$ and $n=0$. One category in which all the $n$-products are defined is called a \textbf{cartesian category}.
In fact, the product can be defined for an arbitrary family of objects indexed by a set $I$:
$$ (X_i)_{i\in I} $$The product would be another object $X$ (usually denoted by $\Pi_{i \in I} X_{i}$) together with a family of morphisms indexed by $I$,
$$ \pi_{i}: X \rightarrow X_{\mathrm{i}} $$satisfying the analogous universal property: for any other object $Y$ and family of morphisms $f_{i}: Y \rightarrow X_{i}$ there exists an unique $g:Y\mapsto X$ such that $f_i=\pi_i \circ g$
A dual notion is that of coproduct in categories.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: